Structured nonnegative matrix factorization for traffic flow estimation of large cloud networks
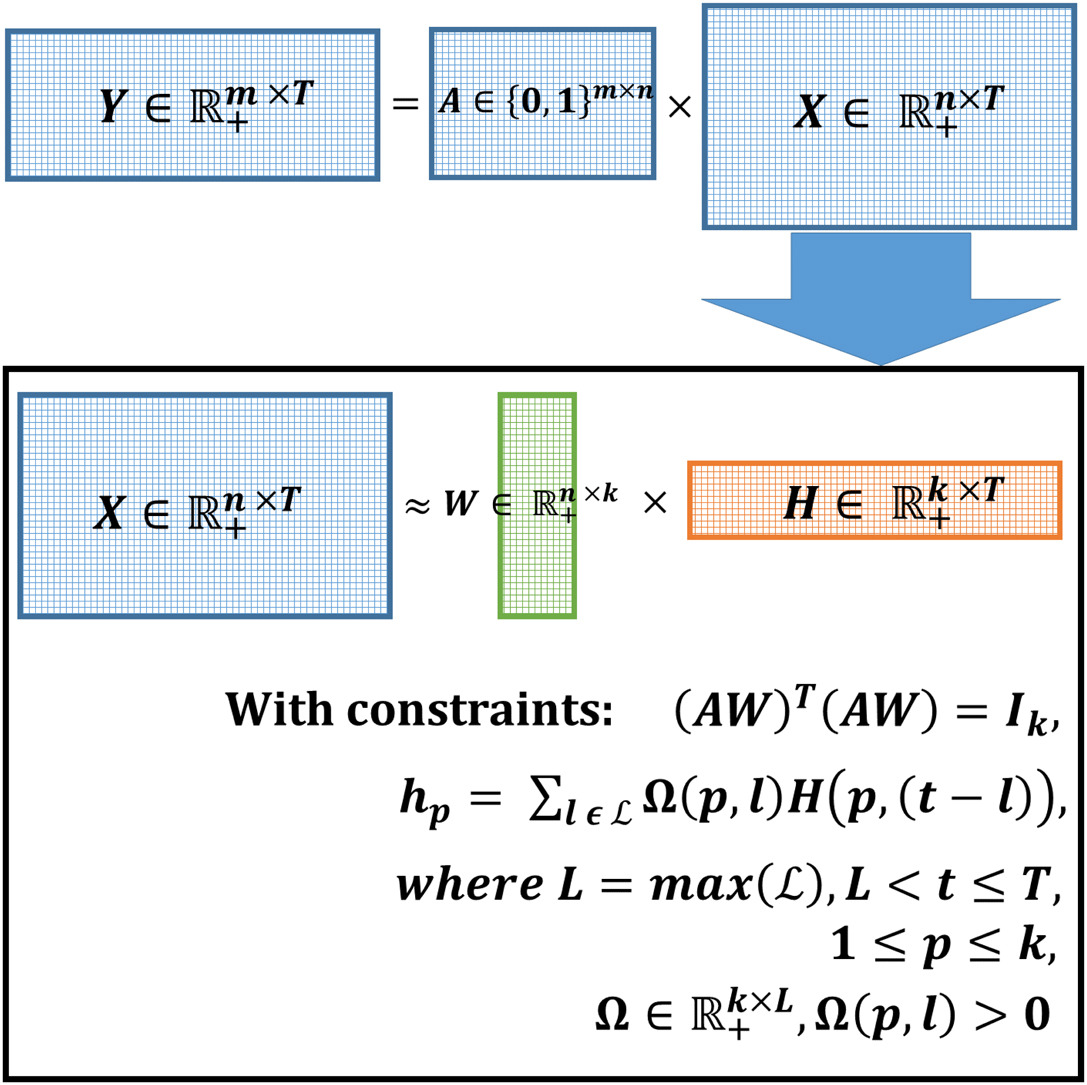
In this paper, we propose a novel model for the network traffic matrix estimation problem which maps high-dimension OD flows to low-dimension latent flows with the following three constraints: (1) nonnegativity constraint on the estimated OD flows, (2) autoregression constraint that enables the proposed model to effectively capture temporal patterns of the OD flows, and (3) orthogonality constraint that ensures the mapping between low-dimensional latent flows and the corresponding link flows to be distance preserving. The parameters of the proposed model are estimated with a training algorithm based on Nesterov accelerated gradient and generally shows fast convergence.